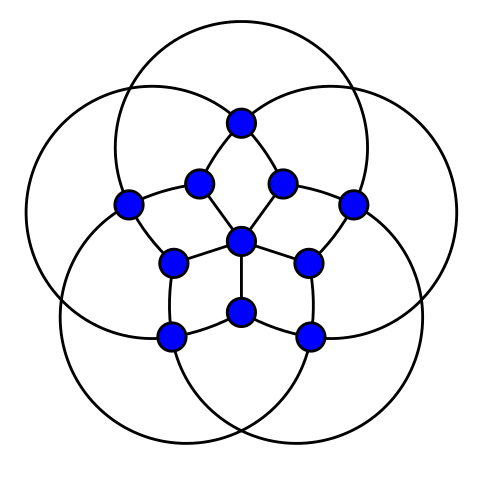
Teoria Grafów

Grafy spotykamy w naszym codziennym życiu na każdym kroku. Sieci połączeń kolejowych, układy scalone, sieci komputerowe, nawigacja a nawet struktury białek w naszym ciele - wszystkie te pojęcia mają wspolną składową, mianowicie można je opisać grafami. Wobec tego zgłębianie własności poszczególnych rodzin grafów ma wiele praktycznych zastosowań i ułatwia optymalne tworzenie obiektów bazujących na grafach.

O tym, jak ważne są grafy w informatyce, uświadomiły takie przedmioty jak Wprowadzenie do Teorii Grafów czy Algorytmy Optymalizacji Dyskretnej. Jest to przykład dziedziny, która choć na pierwszy rzut oka wydaje się niepraktyczna ze względu na silną matematyczną abstrakcję, to jednak z roku na rok staje się co raz bardziej istotna. Uważam, że kazdy informatyk myślący poważnie o pisaniu optymalnego kodu powinien być zaznajomiony z podstawami Teorii Grafów.

Algorytmy Optymalizacyjne

W dzisiejszych czasach wszystkim zależy na wydajności. Pragniemy jak najszybciej dostać się z punktu A do punktu B, fabryki chcą jak najbardziej zminimalizować koszty produkcji, a firmy spedycyjne planują trasy tak, by ich koszt był jak najmniejszy. Z pomocą przychodzą algorytmy znajdujące rozwiązania optymalne (lub sub-optymalne gdy problem jest za trudny).

Dziedzina algorytmów optymalizacyjnych jest bardzo szeroka. Zaliczyć do niej można m.in. algorytmy programowania liniowego, heurystyki i metaheurystyki (przydatne dla problemów NP-trudnych), programowanie dynamiczne, algorytmy aproksymacyjne i wiele, wiele innych kategorii. Przykładowo, na ilustracji obok znajduje się jedno z możliwych rozwiązań problemu komiwojażera. Polega on na tym, że chce znaleźć trasę (cykl) łączącą wszystkie punkty, która będzie miała najmniejszą długość. Problem komiwojażera jest problemem NP-trudnym, sprawdzenie wszystkich możliwości dla choćby czterdziestu wierzchołków połączonych każdy z każdym daje nam aż \(40! \approx 10^{48}\) potencjalnych tras do sprawdzenia, co rzędowo jest porównywalne z liczbą wszystkich atomów na Ziemi. Widać zatem, że bezmyślne sprawdzanie wszystkiego doprowadzi nas do nikąd, potrzeba sprytnych algorytmów korzystających z pewnych heurystyk zmniejszających liczbę przeszukiwanych rozwiązań.

Przykład – sformułowanie problemu komiwojażera jako zagadnienie ILP

Problem komiwojażera możemy zamodelować z wykorzystaniem programowania liniowego całkowitoliczbowego. Niech \(x_{ij}\) będzie zmienną decyzyjną określającą czy krawędź \((i,j)\) została wzięta w rozwiązaniu problemu. Dany jest zbiór wierzchołków \(V = \{1,2,\dots,n\}\) oraz macierz kosztów krawędzi \(C = [c_{ij}]_{(i,j)\in V \times V}\). Model ILP zapisać możemy następująco:
minimize: $$ \sum_{i=1}^{n} \sum_{j=1, j\neq i}^{n} x_{ij}c_{ij} $$ subject to: $$ x_{ij} \in \{0,1\} $$ $$ \sum_{j=1, j\neq i}^{n} x_{ij} = 1 $$ $$ \sum_{j=1, j\neq i}^{n} x_{ji} = 1 $$ $$ \left(\forall Q \subseteq V : |Q| \geq 2\right) \left(\sum_{i\in Q}\sum_{j\in Q}x_{ij} \leq |Q| - 1 \right) $$ Ostatni warunek jest upewnieniem się, że jest tylko jeden główny cykl składający się z wszystkich wierzchołków (sformułowanie Dantziga–Fulkersona–Johnsona).

Uzyskany w ten sposób model możemy rozwiązać z wykorzystaniem różnych metod, np. metody ,,branch and bound". Oczywiście stosowanie takiego modelu dla dużych instancji jest skazane na niepowodzenie – jest to problem NP-trudny. Dla dużych instancji warto zaimplementować algorytmy metaheurystyczne, np. Tabu Search z różnymi wersjami sąsiedztw do wzmocnienia zarówno dywersyfikacji, jak i intensyfikacji przeszukiwań przestrzeni rozwiązań.

A poza studiami?

Lubię gry komputerowe i książki; gdybym miał wskazać swoje trzy najbardziej ulubione gry, to byłyby to Wiedźmin 3 Dziki Gon (w tym minigrę w gwinta obecną w grze), Minecraft (ze względu na nieograniczone pokłady kreatywności drzemiące w tej grze) oraz Portal 2. Jeśli chodzi o książki to staram się nie ograniczać w jednym gatunku, zdarza mi się czytać fantasy, powieści historyczne, kryminalne czy dokumenty.