Przykładowe projekty zrealizowane przeze mnie
Kompilator imperatywnego języka programowania
Celem projektu było stworzenie kompilatora tłumaczącego pewien imperatywny język programowania (sztucznie wymyślonego) na język zadanej maszyny wirtualnej. Zadanie to utwierdziło mnie w przekonaniu, że przekładanie języków to skomplikowany proces.
Na wstępie należało dokonać analizy leksykalnej, stworzyć leksera, który dokona tokenizacji pliku źródłowego. Następnie tokeny wprowadza się do parsera, który analizuje je w kontekście zadanej w parserze gramatyki. To na tym etapie wyświetlane są błędy składniowe. Dla tych dwóch etapów skorzystałem z pakietu SLY dla języka programowania Python.
Ostatecznym i głównym elementem jest sam kompilator tworzący zestaw instrukcji wejściowy dla maszyny wirtualnej. Każdą operację, która wydaje się oczywista i trywialna dla osoby piszącej w wysokopoziomowym języku programowania, trzeba przełożyć na podstawowe instrukcje. Lista dostępny instrukcji maszyny wirtualnej była bardzo uboga, nawet mnożenie trzeba było samemu zaprogramować w sposób optymalny! Należało także zadbać o poprawne wyłapywanie błędów takich jak redeklaracja zmiennej, użycie niezadeklarowanej zmiennej lub procedury czy też podanie niewystarczającej liczby argumentów w procedurze.
def __expression_times(self, x, l):
(value1_data, value2_data) = x
value1_info = value1_data[1]
value2_info = value2_data[1]
value1_codes = value1_data[0]
value2_codes = value2_data[0]
codes = []
if (value2_info == '2'):
codes += value1_codes
var_address = self.symbol_table.getVariableAddress(Variable(value1_info, self.current_proc_name), l)
if not self.symbol_table.isVarInitiated(var_address, l):
Errors.uninitiated(value1_info, l)
codes += [Code(f'LOAD {var_address}')]
codes += [Code(f'ADD {var_address}')]
elif (value1_info == '2'):
codes += value2_codes
var_address = self.symbol_table.getVariableAddress(Variable(value2_info, self.current_proc_name), l)
if not self.symbol_table.isVarInitiated(var_address, l):
Errors.uninitiated(value2_info, l)
codes += [Code(f'LOAD {var_address}')]
codes += [Code(f'ADD {var_address}')]
elif (value1_info == '0' or value2_info == '0'):
codes += [Code(f'SET 0')]
elif (value2_info == '1'):
codes += value1_codes
var_address = self.symbol_table.getVariableAddress(Variable(value1_info, self.current_proc_name), l)
if not self.symbol_table.isVarInitiated(var_address, l):
Errors.uninitiated(value1_info, l)
codes += [Code(f'LOAD {var_address}')]
elif (value1_info == '1'):
codes += value2_codes
var_address = self.symbol_table.getVariableAddress(Variable(value2_info, self.current_proc_name), l)
if not self.symbol_table.isVarInitiated(var_address, l):
Errors.uninitiated(value2_info, l)
codes += [Code(f'LOAD {var_address}')]
else:
codes += value1_codes
codes += value2_codes
if not (Variable('POM_a', self.current_proc_name) in self.symbol_table.addresses_main):
self.symbol_table.addVariable(Variable('POM_a', self.current_proc_name, True), l)
address_pom_a = self.symbol_table.getVariableAddress(Variable ('POM_a', self.current_proc_name), l)
if not (Variable('POM_b', self.current_proc_name) in self.symbol_table.addresses_main):
self.symbol_table.addVariable(Variable('POM_b', self.current_proc_name, True), l)
address_pom_b = self.symbol_table.getVariableAddress(Variable ('POM_b', self.current_proc_name), l)
if not (Variable('POM_res', self.current_proc_name) in self.symbol_table.addresses_main):
self.symbol_table.addVariable(Variable('POM_res', self.current_proc_name, True), l)
address_pom_res = self.symbol_table.getVariableAddress(Variable ('POM_res', self.current_proc_name), l)
if not (Variable('POM_help', self.current_proc_name) in self.symbol_table.addresses_main):
self.symbol_table.addVariable(Variable('POM_help', self.current_proc_name, True), l)
address_pom_help = self.symbol_table.getVariableAddress(Variable ('POM_help', self.current_proc_name), l)
address_a = self.symbol_table.getVariableAddress(Variable (value1_info, self.current_proc_name), l)
address_b = self.symbol_table.getVariableAddress(Variable (value2_info, self.current_proc_name), l)
codes += [Code(f'LOAD {address_a}')]
codes += [Code(f'JZERO', 26, self.labeler.new_label('times_JZERO'))] #wyskocz gdy a = 0!!!
codes += [Code(f'STORE {address_pom_a}')]
codes += [Code(f'LOAD {address_b}')]
codes += [Code(f'JZERO', 23, self.labeler.new_label('times_JZERO'))] #wyskocz gdy b = 0!!!
codes += [Code(f'STORE {address_pom_b}')]
codes += [Code(f'SET 0')]
codes += [Code(f'STORE {address_pom_res}')] # result = 0
codes += [Code(f'LOAD {address_pom_b}')]
codes += [Code('HALF')]
codes += [Code(f'STORE {address_pom_help}')]
codes += [Code(f'ADD {address_pom_help}')]
codes += [Code(f'STORE {address_pom_help}')]
codes += [Code(f'LOAD {address_pom_b}')]
codes += [Code(f'SUB {address_pom_help}')]
codes += [Code(f'JZERO', 4, self.labeler.new_label('times_JZERO'))] # sprawdzenie czy b % 2 == 0
codes += [Code(f'LOAD {address_pom_res}')] # tylko gdy b % 2 != 0
codes += [Code(f'ADD {address_pom_a}')]
codes += [Code(f'STORE {address_pom_res}')] # result += pom_a
codes += [Code(f'LOAD {address_pom_a}')] # to już w obu przypadkach modulo
codes += [Code(f'ADD {address_pom_a}')]
codes += [Code(f'STORE {address_pom_a}')] # pom_a *= 2
codes += [Code(f'LOAD {address_pom_b}')]
codes += [Code(f'HALF')]
codes += [Code(f'STORE {address_pom_b}')] # pom_b /= 2
codes += [Code(f'JPOS', -16, self.labeler.new_label('times_JPOS'))] # gdy pom_b > 0 to powtarzamy procedure
codes += [Code(f'LOAD {address_pom_res}')] # gdy pom_b = 0 to wczytujemy wynik
return codes, value2_infoMetoda obrazująca przekład mnożenia na język maszynowy.
Badanie i implementacja algorytmów metaheurystycznych dla TSP
W parze z Mikołajem Dyblikiem, w ramach przedmiotu algorytmy metaheurystyczne, zajmowałem się optymalizacją wyznaczania możliwie jak najkrótszych tras dla problemu komiwojażera (Travelling Salesman Problem).
Problem komiwojażera jest problemem NP-trudnym, nie istnieje metoda rozwiązująca ten problem za każdym razem w czasie wielomianowym. W związku z tym, wartościowe jest korzystanie z heurystyk i metaheurystyk, które pozwolą na uzyskanie w sensownym czasie jakościowego rozwiązania.
Zaczęliśmy od podstawowych heurystyk, takich jak np. zachłanna heurystyka najbliższego sąsiada. Następnie, zaimplementowaliśmy algorytm Tabu Search dla rożnych rodzajów sąsiedztw (w tym wariant algorytmu korzystający na zmianę z kilku sąsiedztw, dający średnio w testach najlepsze wyniki). Ostatecznie, projekt sfinalizowany został algorytmem genetycznym, gdzie osobniki (tutaj ścieżki zgodne z problemem) walczą o przetrwanie i krzyżują się w celu uzyskania najlepszego rozwiązania.
public Integer[] findSolution() {
timeWhenStarted = System.currentTimeMillis();
generationNo = 0;
listToShuffle = initList(problemSize);
population = generateStartingPopulationWithTournament((int) Math.sqrt(populationSize));
Integer[] bestSolution = population.get(0).clone();
double smallestValue = graph.pathLength(population.get(0));
do {
generationNo++;
List<Pair<Integer[], Integer[]>> parents = generateParentsWithRoulette();
List<Integer[]> children = new ArrayList<>();
if (typeOfCrossoverOperator == 1) {
children = crossoverPMX(parents);
}
population.addAll(children);
List<Integer[]> mutatedPopulation = mutate(population);
List<Integer[]> memedPopulation = memeticAlgorithm(mutatedPopulation);
List<Pair<Integer[], Double>> survivorsWithValues = selectToSurviveWithValue(memedPopulation);
Pair<Integer[], Double> bestSolutionWithValue = getTheBestOne(survivorsWithValues);
if (bestSolutionWithValue.getSecond() < smallestValue) {
bestSolution = bestSolutionWithValue.getFirst().clone();
smallestValue = graph.pathLength(bestSolution);
double averageValueOfPopulation = getAverageValue(survivorsWithValues);
}
population = getSurvivors(survivorsWithValues);
}
while (!stopCriterion(System.currentTimeMillis()));
return bestSolution;
}Fragment kodu algorytmu genetycznego zaimplementowanego w języku Java.
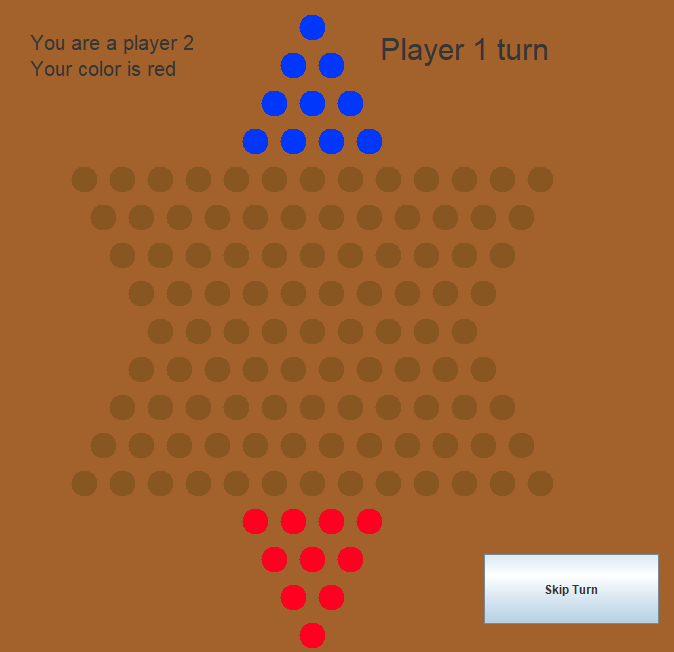
Chińskie warcaby - aplikacja okienkowa w języku Java
Razem z Wojciechem Rymerem napisaliśmy aplikcję do gry w chińskie warcaby. Wykorzystaliśmy do tego Javę z Mavenem, narzędziem bazującym na koncepcie Project Object Model. W implementacji pomocne były wzorce projektowe takie jak Builder, Mediator, Factory czy State.
Aplikacja działa na podstawowym połączeniu Socket dostępnym w bazowych bibliotekach Javy. Największym wyzwaniem, poza samym projektowaniem klas i stosowaniem wzorców, było stworzenie algorytmu walidującego poprawność ruchu. Ponieważ w warcabach możliwe jest wielokrotne bicie, musiał on być rekursywny, ale w taki sposób, żeby się nie zapętlił, co wymagało przechowywania swego rodzaju listy ruchów zakazanych, bo już wykonanych.